CHAPTER 1 : Number system conversion and Complement number

BY = MOHD AKMAL ZAKWAN BIN MOHD ZAKI ( B031210072)


CHAPTER 1 : Number system conversion and Complement number 

Number system conversion

The focus is only at number system conversion of decimal, binary and hexadecimal. Many converting method can be apply for the number system. The most method of convert by using repeated division base 2, 10 and 16.

Binary System

•The binary system is based on 2.
•There are only two digits:  0 and 1•We convert a number from binary to decimal by multiplying each binary digit by its corresponding power of 2.  i.e.  Multiply the bit at position n (n = 0, 1, 2, …) by ( 2 power of n)

Binary to Decimal Conversion

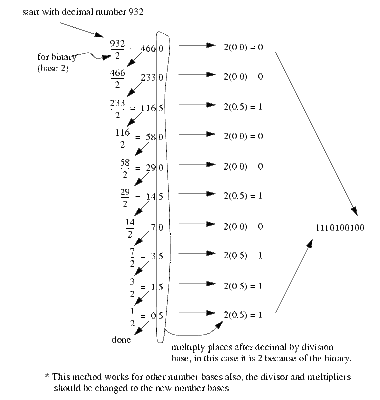
Decimal  to Binary

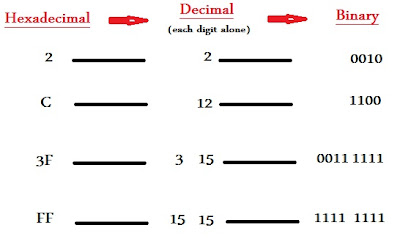
Hexadecimal to Decimal 

Decimal to hexadecimal 

Binary to Hexadecimal

Complement number 

Adding two values is straight forward. Simply align the values on the least significant bit and add, propagating any carry to the bit one position left. If the carry extends past the end of the word it is said to have "wrapped" around, a condition called an "end-around carry". When this occurs, the bit must be added back in at the right-most bit. This phenomenon does not occur in two's complement arithmetic.

  0001 0110     22
+ 0000 0011      3
===========   ====
  0001 1001     25

Subtraction is similar, except that borrows are propagated to the left instead of carries. If the borrow extends past the end of the word it is said to have "wrapped" around, a condition called an "end-around borrow". When this occurs, the bit must be subtracted back in at the right-most bit. This phenomenon does not occur in two's complement arithmetic.

  0000 0110      6
− 0001 0011     19
===========   ====
1 1111 0011    −12    —An end-around borrow is produced, and the sign bit of the intermediate result is 1.
- 0000 0001      1    —Subtract the end-around borrow back into the result.
===========   ====
  1111 0010    −13    —The correct result (6 − 19 = -13)

It is easy to demonstrate that the bit complement of a positive value is the negative magnitude of the positive value. The computation of 19 + 3 produces the same result as 19 − (−3).

Add 3 to 19.

  0001 0011     19
+ 0000 0011      3
===========   ====
  0001 0110     22

Subtract −3 from 19.

  0001 0011     19
− 1111 1100     −3
===========   ====
1 0001 0111     23    —An end-around borrow is produced.
- 0000 0001      1    —Subtract the end-around borrow back into the result.
===========   ====
  0001 0110     22    —The correct result (19 - (-3) = 22).