Chapter 1 : Arithmetics for Computers (Number Systems and Number Operations)

1.1.1 Binary Number System

By : Muhamad Muhaimin Bin Minhad (B031210244)


Computers use binary digits. And some puzzles can be solved using binary numbers.
A Binary Number is made up of only 0s and 1s.

110100

Example of a Binary Number

There is no 2,3,4,5,6,7,8 or 9 in Binary!

How do we Count using Binary?

Binary
0		We start at 0
1		Then 1
???		But then there is no symbol for 2 ... what do we do?

		Decimal
Well how do we count in Decimal?		0		Start at 0
		...		Count 1,2,3,4,5,6,7,8, and then...
		9		This is the last digit in Decimal
		10		So we start back at 0 again, but add 1 on the left

The same thing is done in binary ...

	Binary
	0		Start at 0
•	1		Then 1
••	10		Now start back at 0 again, but add 1 on the left
•••	11		1 more
••••	???		But NOW what ... ?

		Decimal
What happens in Decimal ... ?		99		When we run out of digits, we ...
		100		... start back at 0 again, but add 1 on the left

And that is what we do in binary ...

	Binary
	0		Start at 0
•	1		Then 1
••	10		Start back at 0 again, but add 1 on the left
•••	11
••••	100		start back at 0 again, and add one to the number on the left... ... but that number is already at 1 so it also goes back to 0 ... ... and 1 is added to the next position on the left
•••••	101
••••••	110
•••••••	111
••••••••	1000		Start back at 0 again (for all 3 digits), add 1 on the left
•••••••••	1001		And so on!

Decimal vs Binary

Here are some equivalent values:

Decimal:	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Binary:	0	1	10	11	100	101	110	111	1000	1001	1010	1011	1100	1101	1110	1111

Here are some larger equivalent values:

Decimal:	20	25	30	40	50	100	200	500
Binary:	10100	11001	11110	101000	110010	1100100	11001000	111110100

"Binary is as easy as 1, 10, 11."

Position

In the Decimal System there are the Units, Tens, Hundreds, etc
In Binary, there are Units, Twos, Fours, etc, like this:

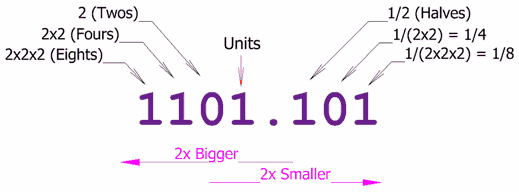This is 1×8 + 1×4 + 0×2 + 1 + 1×(1/2) + 0×(1/4) + 1×(1/8) = 13.625 in Decimal

Numbers can be placed to the left or right of the point, to indicate values greater than one or less than one.

10.1
	The number to the left of the point is a whole number (10 for example)
As we move further left, every number place gets 2 times bigger.
	The first digit on the right means halves (1/2).
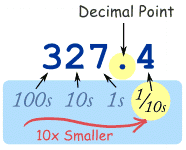
	As we move further right, every number place gets 2 times smaller (half as big).   1.1.2 Decimal Number System A Decimal Number (based on the number 10) contains a Decimal Point. Place Value To understand decimal numbers you must first know about Place Value. When we write numbers, the position (or "place") of each number is important. In the number 327: the "7" is in the Units position, meaning just 7 (or 7 "1"s), the "2" is in the Tens position meaning 2 tens (or twenty), and the "3" is in the Hundreds position, meaning 3 hundreds. "Three Hundred Twenty Seven" As we move left, each position is 10 times bigger! From Units, to Tens, to Hundreds ... and ... As we move right, each position is 10 times smaller. From Hundreds, to Tens, to Units But what if we continue past Units? What is 10 times smaller than Units? 1/10 ths (Tenths) are! But we must first write a decimal point, so we know exactly where the Units position is: "three hundred twenty seven and four tenths" but we usually just say "three hundred twenty seven point four" And that is a Decimal Number! Decimal Point The decimal point is the most important part of a Decimal Number. It is exactly to the right of the Units position. Without it, we would be lost ... and not know what each position meant. Now we can continue with smaller and smaller values, from tenths, to hundredths, and so on, like in this example: 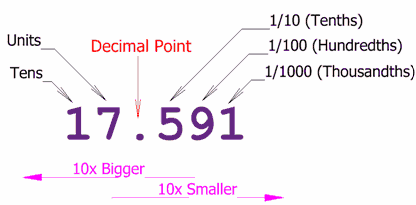Large and Small So, our Decimal System lets us write numbers as large or as small as we want, using the decimal point. Numbers can be placed to the left or right of a decimal point, to indicate values greater than one or less than one. 17.591 The number to the left of the decimal point is a whole number (17 for example) As we move further left, every number place gets 10 times bigger. The first digit on the right means tenths (1/10). As we move further right, every number place gets 10 times smaller (one tenth as big). 1.1.3 Hexadecimal Number System A Hexadecimal Number is based on the number 16 16 Different Values There are 16 Hexadecimal digits. They are the same as the decimal digits up to 9, but then there are the letters A, B, C, D, E and F in place of the decimal numbers 10 to 15: Hexadecimal: 0 1 2 3 4 5 6 7 8 9 A B C D E F Decimal: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 So a single Hexadecimal digit can show 16 different values instead of the normal 10. 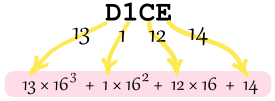Example: What is the decimal value of the hexadecimal number "D1CE" = 53,248 + 256 + 192 + 14 = 53,710 The Point ! Example: 2E6.A3 This is 2×16×16 + 14×16 + 6 + 10/16 + 3/(16×16) Read below to find out why Numbers can be placed to the left or right of the point, to indicate values greater than one or less than one: The number just to the left of the point is a whole number, we call this place units. As we move left, every number place its 16 times bigger. The first digit on the right of the point means sixteenths (1/16). As we move further right, every number place its 16 times smaller (one sixteenth as big).